РАВНОВЕСИЕ ТЕЛА
Спасибо нашим инвесторам из казино онлайн
РАВНОВЕСИЕ ТЕЛА
. I. Р. м е х ан и ч е с к о е, состояние, при к-ром тело не испытывает никакого ускорения. В более узком, практически обычно применяемом смысле Р. т. есть состояние неподвижности его относительно окружающей среды. Для того, чтобы неизменяемое (жесткое) тело находилось в равновесий, необходимо и достаточно: а) чтобы геометрическая (т. е. полученная путем последовательного применения правила параллелограмма) сумма всех сил, действующих на точки этого тела, была равна нулю и б) чтобы геометрическая сумма всех моментов сил, действующих на тело, была также равна нулю. Если тело нельзя считать неизменяемым, то условия Р. т. становятся сложнее. Такое тело приходится мысленно разбить на элементы, достаточно малые для того, чтобы можно было считать их применительно к поставленной задаче неизменяемыми телами; для Р. т. необходимо в этом случае, чтобы условия а) и б) выполнялись для каждого элемента в отдельности. Т. о. если число элементов равно
п,
то для Р. т. необходимо, чтобы были выполнены 2
п
независимых друг от друга условий. Если сумма сил, действующих на неизменяемое тело, не равна нулю, то мы всегда можем сделать ее нулем, приложив к телу еще одну силу, равную и противоположную упомянутой сумме сил. Такую силу, приводящую тело в равновесие, называют уравновешивающейсилой. Для приведения в равновесие сложной системы из
п
элементов необходимо иметь в своем распоряжении
п
уравновешивающих сил и столько же уравновешивающих моментов. На практике очень часты случаи, когда силы и моменты, действующие на тело, определенным образом зависят от положения, занимаемого телом в пространстве. Напр. при перемещении куска железа в силовом поле магнита сила притяжения последнего тем больше, чем ближе железо к полюсу магнита. При сообщении подвешенному маятнику различных наклонов момент силы тяжести, действующей на маятник, тем больше, чем ближе нить маятника к горизонтальному положению, и тем меньше, чем она ближе к вертикали. В этих случаях среди многочисленных других положений могут существовать и такие, при к-рых суммы сил и суммы моментов, действующих на тело, обращаются в нуль. Такие положения называются положениями равновесия. В зависимости от того, как действуют на тело силы и моменты в ближайшей окрестности от положения равновесия, различают три разновидности положений Р. т.: п о л о ж е н и я б е з р а 3 л и ч-ного, устойчиво го и не устойчиво го Р. т. В первом случае все положения в ближайшей окрестности от данного положения Р. т. сами суть точно так же положения Р. т. Во втором случае в любой близости. от данного положения Р. т. имеются положения, лишенные равновесия, но только такие, из к-рых силы и моменты гонят тело к положению Р. т. Наконец в третьем случае в любой близости от данного положения Р. т. имеются неуравновешенные положения, не связанные ограничивающим условием второго случая. Поведение тела вблизи от положений равновесия этих трех видов известно из элементарной физики. Особенно важное значение для прикладной механики и для биомеханики имеет тот случай, когда все силы, действующие на точки тела, остаются всегда постоянными по величине и параллельными между собой: таковы прежде всего силы тяжести. В этом случае сила, уравновешивающая все такие параллельные и постоянные силы, проходит всегда через одну и ту же точку неизменяемого тела, называемую центром тяжести тела, в каком бы положении само это тело ни находилось. Для изменяемых тел уравновешивающая сила для сил типа тяжести точно так же постоянна по величине и по направлению, но может проходить через различные точки изменяемого тела, в зависимости только от его деформаций, а не от положений его в пространстве: в изменяемых телах положение центра тяжести непостоянно. Если неизменяемое тело подвесить за какую-либо точку, то его состояние равновесия или неравновесия под действием тяжести целиком определится тем, какое положение будет занимать его центр тяжести по отношению к точке подвеса: 1) тело будет в равновесии, если центр тяжести лежит на одной вертикали с точкой-подвеса, и Не будет в равновесии во всяком другом случае; 2) равновесие будет устойчивое, если центр тяжести находится ниже Точки подвеса, неустойчивое, если он выше, и безразличное, если он совпадает с точкой подвеса, т. е. если тело подвешено за самый центр тяжести. II. Р. б и о м е х а н и ч е с к о е. 1. Равновесие в сочленении. Звено
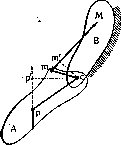
А
(рис. 1) может вращаться относительно звена
В
в соединяющем их сочленении с. Если одно из звеньев, напр.
В,
закреплено не
подвижно, то для равновесия звена
А
необходимо и достаточно, чтобы моментывеех сил, действующих наразлич-ные точки звена
А
, вычисленные по отношению к центру сочленения с, были в сумме равны нулю. Допустим для простоты, что на звено
А
действуют 2 силы: сила тяжести Р и сила мышечной тяги
М
(рис. 1). Первая сила приложена в центре тяжести звена
р
и представляет собой равнодействующую (т. е. геометрическую сумму) всех сил тяжести, действующих на отдельные точки звена. Вторая сила представляет собой равнодействующую всех сил, развиваемых отдельными во-Р локнами данной мышцы, и проходит через нек-рую точку звена
т,
лежащую на площади прикрепления мышечного сухожилия к кости. Момент силы Р относительно точки
с
равен произведению силы на плечо ее действия, т. е.на длину перпендикуляра
ср
Допущенного из центра сочленения на линию действия силы Р. Легко убедиться, что, если изобразить силу
Р
стрелкой в определенном масштабе, то момент ее относительно с будет численно равен площади параллелограмма, построенного на прямых отрезкахР
яср
(рис.2).Рассуждая та –
Рисунок 1

величины
ким же образом, определяют момент’силы
М
как произведение
М
на
cm’,
т. е. как|величину, численно равную площади параллелограмма, построенного на
М
и
ст.
Для того чтобы звено
А
было в равновесии, необходимо, чтобы моменты
Р. ср’яМ. cm’
были, равны и противоположно направлены, иначе говоря, чтобы упомянутые выше два параллелограмма были равновелики и располагались бы по обеим сторонам от звена
А.
—Если на звено
А
действуют не две, а несколько сил, то ход рассуждения и расчета остается тем же самым, только приходится просуммировать (геометрически) не два, а несколько моментов, рассчитанных вышеописанным образом. На рис. 3 изображено звено
А,
на которое действуют 4 независимые силы: Р—сила тяжести звена,
Q
—сила тяжести дистального звена
D, F
—сила мышцы-флексора и
Е
—силамышцы-экстенсора. Звено будет в равновесии, еЪли сумма моментов всех этих 4 сил относительно точки
с
равна нулю. Необходимо подчеркнуть, что во всех примерах этого рода Р. т. определяется не весами звеньев, к-рые суть длительно-постоянные моментами этих весов, к-рые меняются в зависимости от положения звена в очень широких пределах. Так, на рис.
4а
момент звена
А
мал, т. к. мало плечо
ср’;
если же повернуть звено
А,
как изображено на рис.46, то плечо ср’возрастет, а с ним возрастет и момент Р.
ср’.
Для длинных звеньев тела (предплечье, плечо, голень, бедро) можно принять, что момент их тяжести имеет наибольшее значение, когда продольные оси их горизонтальны, и близок к нулю, когда они вертикальны. Итак, хотя веса звеньев и постоянны, но моменты их,
Р. ср’,
изменчивы так же, как и моменты мышечных сил,
М. cm’.
Поэтому для уравновешивания этих моментов между собой организм может прибегать к изменению как тех, так и других. Если напр. на рис. 3 геометрическая сумма (т. е. в данном примере разность) моментов мышц-антагонистов
F
и
Е
больше самого большого значения, какое может принять общий момент сил тяжести Р и
Q
(при горизонтально вытянутых звеньях), то равновесие невозможно, и система звеньев 1иБ должна начать двигаться в направлении флексии. Если же эта сумма мышечн. моментов будет принимать любые меньшие значения, лежащие между упомянутым максимумом момента тяжести и нулем, то для каждого из этих значений найдутся такие расположения звеньев
А
и
D,
при которых система окажется в равновесии. В огромном большинстве случаев система сама придет в это положение, как только сумма мы –
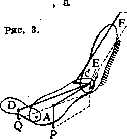
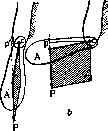
Рис.

шечных моментов приняла известное значение. Точно так же можно утверждать, что для каждого положения системы звеньев Ая D существует такое значение суммы мышечных моментов, которое уравновешивает систему в заданном положении.
Описанные выше перемещения системы звеньев до положения равновесия, заданного определенным мышечным моментом, имеют огромное, если не преобладающее значение в биомеханике движений. Этим движениям присвоены названия статико-динамич. или фиксационных или фиксированных, а состояния равновесия, наступающие в результате их, называются статич. положениями, состояниями статич. работы или фиксациями. Чисто динамические движения звеньев, т. е. такие, при к-рых конечность движется ускоренно, не проходя через положение равновесия и не останавливаясь, пока не наткнется на какое-либо внешнее препятствие (удар), на практике сравнительно редки. Гораздо чаще случаи фиксационных движений, к к-рым относится преобладающее большинство профессиональных движений. В качестве частного случая разобранного закона следует указать, что, если сумма мышечных моментов равна нулю, то для равновесия системы звеньев
A, D
и т. д. необходимо, чтобы и сумма моментов их сил тяжести, т. е. P. cp’,
Q. cq’
и т. д. (рис. 5), была также равна нулю. Это последнее условие выполняется тогда, когда общий центр тяжести системы звеньев
A, D:.
лежит на одной вертикали с точкой подвеса системы (в данном случае— с центром сочленения с); равновесие системы будет устойчивым или неустойчивым в зависимости от того, находится ли общий центр тяжести системы ниже или выше точки опоры системы с. Из этого частного случая следует, что, когда мышцы сочленения с бездействуют (их общий момент = 0),»то центр тяжести подвешенной к с системы обязательно расположится на одной вертикали с точкой с, т. е. приведет систему в состояние устойчивого равновесия, и с этой вертикали его не смогут согнать никакие сокращения мышц системы, не перекидывающихся через точку с (т. н. внутренних мышц системы), хотя бы за счет этих сокращений сама система претерпевала самые разнообразные деформации. В наиболее общей форме это крайне важное для учения о движениях правило выражается так: внутренние мышцы, системы могут смещать центр тяжести системы только вдоль прямой линии, соединяющей его положение с точкой опоры или подвеса. 2.Равновесие всего тела человека. Р. т. стоящего человека можно рассматривать с совершенно тех же точек зрения, с каких выше было рассмотрено равновесие отдельных систем звеньев. В данном случае системой звеньев будет все тело, но вместо точки опоры
с
мы будем иметь дело с площадью опоры
С
(рис. 6), состоящей ив контуров опирания обеих стоп и из площадки, заключенной между ними. Т. к. между телом и поверхностью опоры при стоянии не перекинуто никаких тяг, подобных мышцам, то очевидно равновесие при стоянии может протекать исключительно только, по образцу последнего разобранного частного случая. Для Р. т. при стоянии необходимо, чтобы момент общего центра тяжести всего тела по отношению к площади опоры
С
был равен нулю, т. е. чтобы вертикаль, опущенная из общего центра тяжести всего тела, проходила через площадь опоры.

Рисунок 6.
Важнейшие следствия из этого основного положения таковы: 1) никакие внутренние силы системы (т. е. никакие сокращения мышц) не могут, согласно сказанному выше, сместить центр тяжести тела с вертикали, на к-рой он находится, т. е. нарушить Р. т., если оно уже существует. Однако, т. к. этот центр тяжести лежит выше поверхности опоры, т. е. равновесие принадлежит к неустойчивому типу, то достаточно уже очень небольшой внешней силы для нарушения этого равновесия. Если бы опора была не площадкой С, а точкой с, то от малейшего внешнего. воздействия (дуновения ветерка) Р. т. нарушалось бы непоправимо, т. е. с этим нарушением не могли бы бороться никакие мышечные сокращения. При наличии площади опоры
С
конечных размеров такое же непоправимое нарушение Р. т. наступает, если внешняя сила выведет вертикаль общего центра тяжести за пределы этой площади. В этом случае человек не может не упасть, если только не изменит своевременно контуров своей площади опоры, напр. не переставит ногу. 2) Если человек держит тяжелый груз, то предыдущее положение остается справедливым по отношению к общему центру тяжести тела и груза. Центр тяжести одного только тела или центр тяжести одного груза может при этом оказаться и не над площадью опоры. 3) Если площадь опоры стояния заменяется линией опоры (канатоходец, велосипедист) или точкой опоры (танцовщица «на пуанте», велосипедист, едущий на одном колесе), то никакое длительное статическое Р. т. немыслимо. В этих случаях оно заменяется динамическим равновесием, или балансированием, принципиальный биомеханический механизм к-рого во всех случаях один и тот же. Как уже подчеркивалось, никакие мышечные сокращения не могут сместить центра тяжести тела с вертикали или вернуть его на эту. вертикаль. Поэтому мышечные сокращения балансирования преследуют всегда совершенно другую цель: они Рисунок 7. стремятся не поставить центр тяжести над точкой опоры, что невозможно, а подвести точку опоры под центр тяжести, что иногда возможно. Танцовщица «на пуанте» балансировать не может, т. к. точка опоры ее носка несмещаема, но на канате, обладающем поперечной подвижностью, балансировать можно. Поэтому-то получается парадоксальная на первый взгляд вещь,,что по канату толщиной в 3
мм
итти можно и сравнительно безопасно, а по балке шириной в 30
мм
крайне опасно, если не невозможно. Балансирование при езде на велосипеде или при беге на коньках сводится все к тому же своевременному подведению линии опоры под центр тяжести. Если велосипед начинает крениться вправо, т. е. центр тяжести оказывается правее линии опоры, то ездок поворачивает руль вправо же, чтобы подкатить велосипед под уклонившийся в эту сторону центр тяжести. Балансировать на стоящем велосипеде нельзя, т. к. при этом его точки опоры становятся нес-мещаемыми. 4) Равновесие при ходьбе относится также к типу динамического равновесия, или балансирования. При начале каждого шага вертикаль центра тяжести выходит за пределы поверхности опоры задней ноги, и начинается падение тела вперед. Задача балансирования сводится здесь к подхватыванию этой вертикали другой ногой, своевременно создающей новую площадь опоры впереди. Рисунок 7 показывает, как движется вертикальная проекция центра тяжести между площадями опоры стол при ходьбе. 3. Меха н-и змы стати чес к ого Р. т. и балансирования. Иннервационные механизмы обеих названных функций вообще разнообразны и кроме того существенно различны для случаев статического и динамического Р. т. Для статического Р. т. в первую очередь существенны нервные механизмы мышечного тонуса, в частности такие явления, как закрепительный или пластический тонус Икскюля (Sperrtonus, Uexkiill), лежащий пови-димому в основе многих фиксаций. Затем следует упомянуть «статический тонус» Брондгеста (Ruhetonus, Brondgeest), представляющий собой весьма сложный рефлекс, вернее совокупность рефлексов, поддерживающих мышцы всего тела в состоянии тех тонических напряжений, к-рые требуются для поддержания Р. т. при той или иной позе. Многочисленные авторы утверждают, что этот тонический эффект протекает без токов действия, под влиянием вегетативных иннервации. (Центральную локализацию этих тонических рефлексов см.
Тонус.)
— Вторую, и несомненно основную, группу иннервации, определяющих собой как статическое Р. т., так и балансирование, составляют пройриоцептивные иннервации и проприоцеп-тивные рефлексы. Эти последние состоят в изменениях напряжений мышц под влиянием раздражений периферических элементов, заложенных в сухожилиях мышц,
в оболочках сочленовных сумок и около самих мышечных волокон. Эти концевые аппараты воспринимают, с одной стороны, изменения положения в пространстве (точнее, изменения взаимного расположения) членов тела; с другой же стороны, они реагируют на силовые изменения в мышцах и сухожилиях, на изменения напряжений в тех и других. Расстройства нормальной деятельности проприоцептивного аппарата (атаксия при поражении задних столбов) влекут за собой столь значительные расстройства Р. т. (симптом Rom-tterg’a), что уже одно это заставляет признать за ним ведущую роль в поддержании равновесия тела. Несомненно, что проприоцептивный аппарат участвует как в осуществлении простейших стат. рефлексов тонич. характера, так и в сложных динамич. актах балансирования. Весьма важную роль в физиологии равновесия играет вестибулярный аппарат, воспринимающий изменения положения головы в поле тяготения и смещения или ускорения; испытываемые ею в пространстве. Будучи связан с одной’только головой, вестибулярный аппарат сам по себе был бы бессилен оказывать содействие поддержанию Р. т. в целом; поэтому его деятельность тесно связана с деятельностью всей проприоцептивной системы, в особенности же с тоническими рефлексами шейной мускулатуры. В этом сочетании на долю-вестибулярного аппарата выпадает главная роль в поддержании Р. т., в особенности при сложных актах балансирования, что делает безупречность его •функционирования непременным условием таких профессий, как напр. профессия летчика.— Наконец следует упомянуть еще о роли мозжечка, обладающего огромным количеством нервных связей и принимающего теснейшее участие во всевозможных актах поддержания Р. т. Есть все основания полагать, что именно моз – жечок является высшим регулирующим центром, к к-рому стекаются все проприоцептивные и вестибулярные импульсы и к-рый через систему клеток передних рогов, а также вероятно через систему п. rubri и симпат. ствол воздействует на состояние мышц, содействуя поддержанию Р. т. Патология Р. т.—см.
Vestibularis nervus, Вестибулярная система, Мозжечок,. Атаксия.
Лит.:
Handbuch der normalen und pathologischen Phy-siologie, hrsg. v. A. Bethe, G. Bergmanu u – a., B. XV, T. i, BewegungundGleichgewicht, B.,1930 (лит.). Н. Бернштейн.